Distribute Coins in Binary Tree

Dec 25, 2021

Problem

你有一個 n 個節點（node）的二元樹 root，每個在二元樹上的 node 有 node.val 枚硬幣，整個二元樹總共有 n 枚硬幣。在每一次的移動中，我們需要選擇兩個相鄰的 node 並且移動一枚硬幣到另一個 node。移動的方式可能是從 parent node 移動到 child node，或者是 child node 到 parent node。回傳讓每個 node 都有一枚硬幣所需要的最小移動次數。

Example 1

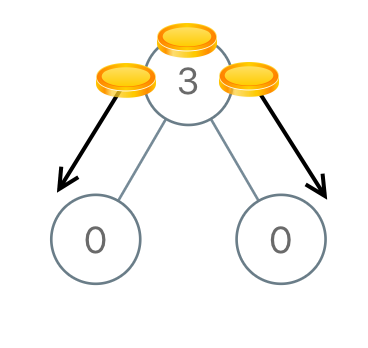
Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2

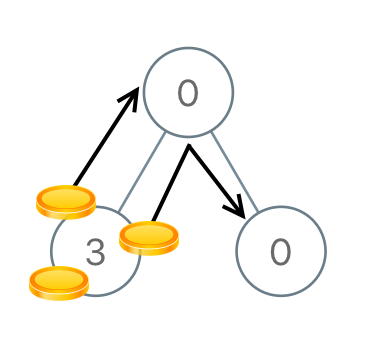
Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Constraints

The number of nodes in the tree is n.
1 <= n <= 100
0 <= Node.val <= n
The sum of all Node.val is n.

Solution

一開始看到這個題目的時候的想法是從二元樹的節點出發去思考，怎麼往下去分配硬幣，但看到 Example 2 的時候就發現自己的想法錯了，因為根節點可能會是沒有任何的硬幣的，那麼該要怎麼做會比較好？

如果 child node 上都沒有任何的硬幣，那代表需要由 parent node 將硬幣分給它；若 child node 有超過一個以上的硬幣，那 node 本身只需要留下一枚，剩下的需要分配到其他沒有硬幣的 node。

以範例一來說，左右的 child node 都沒有任何的硬幣，那麼就需要從 parent node 分別個移動一個硬幣到左右的 child node，所以移動的次數會是 1 + 1 = 2 次；在範例二當中，可以看到示意圖是從左邊的 child node 出發來移動硬幣，因為 parent node 本身沒有硬幣所以無法分配，根據這兩個範例可以推論出硬幣的分配是：

取決於子節點（Child Node）

根據題目要求要找到最小的移動次數，移動包含了「移入」和「移出」的動作，這些動作都被視為一次的操作：

// move might be a negative number
abs(move)

透過 steps 變數來記錄每次移動的次數：

func distributeCoins(root *TreeNode) int {
  steps := 0
  dfs(root, &steps)
  return steps
}

而 dfs 函式就是整個問題求解的核心。

Implementation

由於是二元樹（Binary Tree)，會使用遞歸（Recursion）來解題。首先找出 Base Case，也就是當 child node 為空的時候，不需要被分配任何硬幣：

func dfs(root *TreeNode, steps *int) int {
+  if root == nil {
+    return 0
+  }
}

接著是 Recursive Case，根據題目可以使用後序遍歷（Post-Order Traversal）：

func dfs(root *TreeNode, steps *int) int {
  if root == nil {
    return 0
  }

+ left := dfs(root.Left, steps)
+ right := dfs(root.Right, steps)

  // Do something...
}

以範例一作為說明搭配著圖來看，把 Do something... 的實作部分補上：

看到左節點本身並沒有包含任何 child node，所以符合 Base Case 所以各回傳 0，也就是不需要任何的移動，可以得到以下計算：

steps = steps + abs(left) + abs(right) // 0 + 0 + 0

接著到了左節點本身，它並沒有任何的硬幣，表示它需要由父節點來分配硬幣，可以得到以下計算：

coins = root.Val - 1 + left + right // 0 - 1 + 0 + 0 = -1， -1 表示需要被分配一枚硬幣

其中 root.Val - 1 代表的意思是節點本身至少要有一枚硬幣。

因為左右兩側節點相同，所以右節點過程會跟上述一樣，所以可以得到此推導：

最後回到根節點，可以推導出：

// implement Do something...
left := dfs(root.Left, steps) // -1，代表需要分配一枚硬幣
right := dfs(root.Right, steps) // -1，代表需要分配一枚硬幣
steps = steps + abs(-1) + abs(-1) // 0 + 1 + 1 = 2，代表需要移動兩次

return root.Val - 1 + left + right // 3 - 1 + (-1) + (-1) = 0

這樣就完成了範例一，讓我們在花一些時間來驗證上述概念套在範例二是否也能找出答案。

範例二一樣先從左節點開始看起：

左節點的 root.Val = 3 且沒有任何的子節點，可以計算出：

左節點本身留一枚硬幣，接著需要移動兩次硬幣到根節點，根節點本身沒有任何硬幣，需要自己留一個，右節點也需要被分配一枚硬幣：

left := dfs(root.Left, steps) // 3 - 1 + 0 + 0 = 2
right := dfs(root.Right, steps) // -1
steps = steps + abs(2) + abs(-1) // 0 + 2 + 1 = 3

return root.Val - 1 + left + right // 0 - 1 + 2 + (-1) = 0

完整實作

func distributeCoins(root *TreeNode) int {
  steps := 0
  dfs(root, &steps)
  return steps
}

func dfs(root *TreeNode, steps *int) int {
  if root == nil {
    return 0
  }

  left := dfs(root.Left, steps)
  right := dfs(root.Right, steps)
  *steps = *steps + abs(left) + abs(right)

  return root.Val - 1 + left + right
}

Reference

🔗 Distribute Coins in Binary Tree